3.12

证明：对任何 $M, N \in \Lambda$，若 $M =_\beta N$，则存在 $T$ 使得 $M \twoheadrightarrow_\beta T$ 且 $N \twoheadrightarrow_\beta T$，即 对于 $=_\beta$ 的 CR 性质

证明

对 $M =_\beta N$ 的归纳长度（结构）做归纳，设长度为 $n$

Basis：$n = 0$，即 $M \equiv N$，取 $T \equiv M$ 或 $T \equiv N$ 即可

I.H. $M =_\beta N$ 的构造长度不大于 $n$ 时，该性质成立

I.S. $M =_\beta N$ 的构造长度为 $(n+1)$，即存在 $P_0, P_1, \cdots, P_{n+1}$ 使得

$P_0\equiv M, P_{n+1}\equiv N, \forall i<n+1. P_i \rightarrow_\beta P_{i+1} \text{ or } P_{i+1}\rightarrow_\beta P_i$

因此，$M=_\beta N$ 有两种可能性：

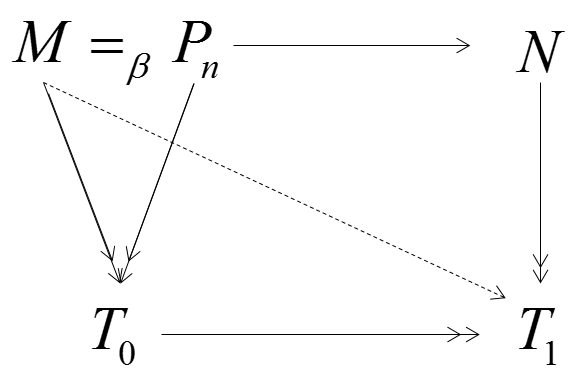
case 1：$M = _\beta P_n \rightarrow_\beta N$

由 I.H. 知，存在 $T_0$ 使得 $M \twoheadrightarrow_\beta T_0, P_n \twoheadrightarrow_\beta T_0$，又因为 $P_n \rightarrow_\beta N$，由 CR property 知，存在 $T_1$，使得 $T_0 \twoheadrightarrow_\beta T_1, N \twoheadrightarrow_\beta T_1$，根据 $\twoheadrightarrow_\beta$ 的传递性，所以 $M \twoheadrightarrow_\beta T_0 \twoheadrightarrow_\beta T_1$，$M \twoheadrightarrow_\beta T_1$，此时 $T_1$ 即为所求

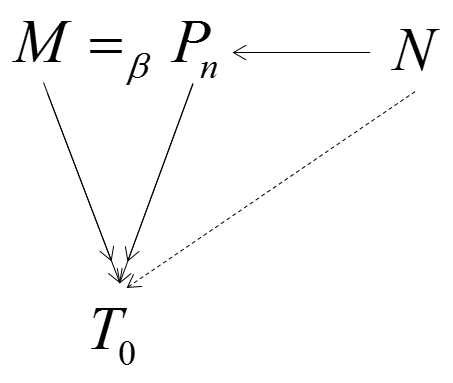
case 2：$M =_\beta P_n{}_\beta\leftarrow N$

由 I.H. 知，存在 $T_0$ 使得 $M \twoheadrightarrow_\beta T_0$ 且 $P_n \twoheadrightarrow_\beta T_0$，又 $N \rightarrow_\beta P_n$，所以 $N \twoheadrightarrow_\beta T_0$，此时 $T_0$ 即为所求